読み方/英語:にしんほう/binary system /にしんすう/binary number
2進法(2進数)とは「0」と「1」だけを使って数を表す方法。
≪2進法/2進数を詳しく説明すると≫

さあ今日は「2進法」について勉強するわよ。

2進法?初めて聞く。

そうね、私たちが普通に暮らしている場合、「2進法」に出会うことはあまり無いわよね。私たちの暮らしで一般的なのは「10進法」よ。

そもそも”〇進法”という言い方になじみが無いから、よくわからんな。

簡単に説明すると、「10進法」は「0」~「9」までの10個の数字で数を表す方法ね。これは私たちが日常使っている方法よ。それに対して2進法は「0」と「1」だけを使って数を表す方法ね。

「0」と「1」だけ。

実はコンピュータの世界は「10進法」ではなくて「2進法」で成り立っているのよ。

「2進法」?
なんで?

それはこの勉強が終わるころには分かるようになるわよ。
ちなみに「〇進法」は「〇進数」と呼ばれる場合があるんだけど、ここでは「〇進法」で統一していくからね。

お願します。
10進法とは

まずは、私たちになじみの深い「10進法」から説明するわね。
「0」「1」「2」「3」「4」「5」「6」「7」「8」「9」の10個の数字を使って数を表すのが「10進法」なの。これは分かるわよね。

当然やな。

例えば、数が「0」から「9」までの時は順番に、
「0」「1」「2」「3」「4」「5」「6」「7」「8」「9」と書けるわ。
ではこの「9」の次は何でしょう?

「9」の次は「10」やろ。あたりまえやん。

そうね、じゃあ次はどうかしら。
「10」「11」「12」「13」「14」「15」「16」「17」「18」「19」
この次は何かしら?

「19」の次は「20」やろ。だからあたりまえやん。

そうね、じゃあ次はどう?
・・・「97」「98」「99」、この次は何かしら?

「99」の次は「100」や。

素晴らしいわ!

おい、馬鹿にしてるやろ?

まあまあ、「10進法」はこんな感じね。
2進法(2進数)とは

では次に「2進法」よ。「2進法」は「0」と「1」の2つの数字だけを使って数を表すのよ。

ふむ。

じゃあ行くわよ。
「0」「1」、この次は何でしょう?

えっと、「1」の次は「2」、あれ「2」は使えんのか。。。

そうよ、「2進法」は「0」、「1」しか使えないのよ。

という事は、もしかして「10」?

そう、正解!やるじゃない。

なるほど。
「10進法」では「9」の次が「10」になるのが、「2進法」やと「1」の次が「10」になるんか~。

その通りよ。
じゃあ、「10」「11」、この次は?

えっと「12」ではなくて、もしかしたら「100」か?

ご名答!すごいわ、さすが理解が早いわね。

なるほど、桁が上がっていくのが早いんやな。まあ数字が2つしかないからな。

そうなの、「10進法」より「2進法」の方が桁が早く増えるわ。
ちょっと文章では分かり難いから表にしてみるわ。
| 10進法 | 2進法 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| … | … |
こんな感じよ。

むむむ。

ここで「10進法」と「2進法」にどんな相関関係があるのが分かるかしら?

何かがありそうな感じやけど、わからん。

「2進法」の桁が増えるごとに、それに対応する「10進法」の値が2倍ずつ増えていくのよ。
さっきの表の太字のところよ。まとめると下図になるわ。
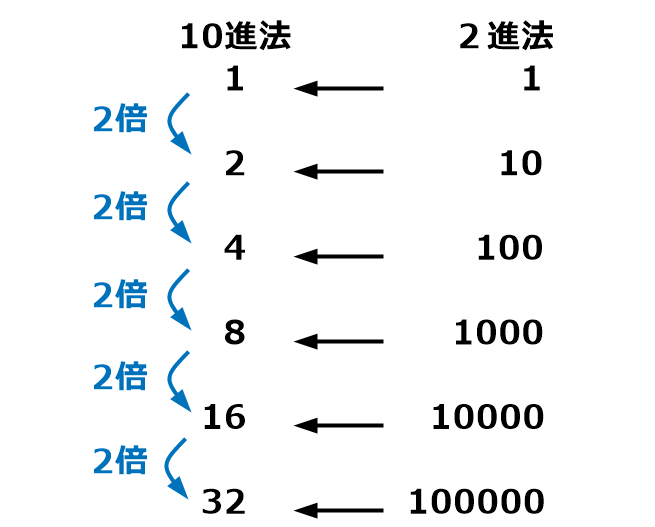

なるほど、こんな関係があるんやな。
でも数学は苦手やな。

この関係を覚えておけば、「2進法」に対する「10進法」の値を無理に暗記する必要は無いのよ。じゃあ次に「2進法」と「10進法」の変換のやり方を説明するわ。

ちょっと質問。
そもそもなぜ「2進法」なんかを知る必要があるんや?

良い質問ね。
それはコンピュータの世界が「2進法」で構成されているからよ。

なんで?
皆が分かる「10進法」にすればええやんか。

そうね、初期のコンピュータの頃は「10進法」を使っていたこともあったみたいだけど、そのうち「0」と「1」のみを使用する「2進法」の方が初期のコンピュータにとって電子的な回路の設計や修理が簡単なので、「2進法」の方に移行していったそうよ。
それらが根付いて今に至るの。

うーむ、そうやったんか。

元々コンピュータはスイッチの「ON」と「OFF」というシンプルな仕組みから始まって、それが「0」と「1」だけの「2進法」につながっていったのよ。

なるほど、わかった。

そういう事で「2進法」を知っておいた方がコンピュータの仕組みをより熟知できると思うので説明していくわ。じゃあ「2進法」と「10進法」の変換のやり方を説明するわよ。

お願いします。でも数学は苦手やな。

そんなに難しくないわ。数学というより算数よ。
「2進法」と「10進法」の変換方法
「2進法」を「10進法」に変換する計算方法

まず「2進法」を「10進法」に変換する計算方法からね。
さっき説明した「10進法」と「2進法」の相関関係を思い出して。下の図よ。


ふむ。

例えば「2進法」の値が”1101”で、それを「10進法」に換算するわ。
まず「2進法」を桁ごとに分解して、それに対応する「10進法」の値を書き出すの。
対応する数値は上の図を見てね。
0の場合はそのまま0となるわ。
最後に10進法の値を合計した値が、換算した値となるのよ。
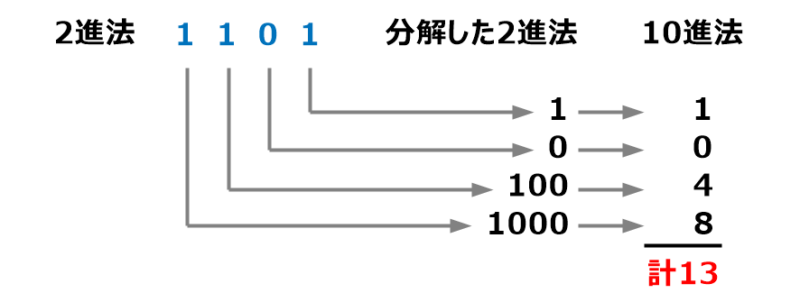

この計算方法で、「2進法」の”1101”は「10進法」の”13”と簡単に算出できるわ。

何とか分かった。

良かったわ。
「10進法」を「2進法」に変換する計算方法

じゃあ次は「10進法」を「2進法」に変換する計算方法を説明するわ。
考え方は、「2進法」の桁が増えるごとに、それに対応する「10進法」の値が2倍ずつ増えていく」という相関関係を逆に応用するわ。
10進法の値を2で割っていくことで、桁ごとに2進法の値に変換して最後に足し合わせるの。

むむむ

例えば「10進法」の値が”14”の場合の「2進法」の値を算出してみるわ。
まず”14”を2で割ってその余りを算出するの。
14÷2=7・・・余り0
次に前回の式の商(余りを除いた結果)を2で割る。
7÷2=3・・・余り1
これを繰り返す。
3÷2=1・・・余り1
1÷2=0・・・余り1
商が0になったら終了よ。
最後にこれらの余りを下から読んでいくと「2進法」の値となるわ。
結果は”1110”よ。
わかりやすい式に直すと下図のようになるわ。
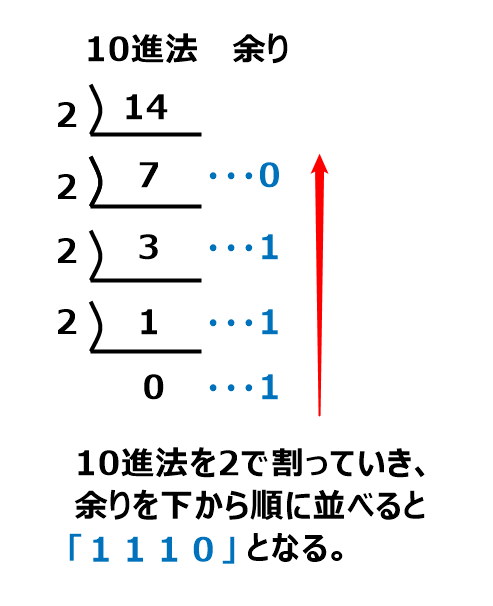

ふむふむ。これが「10進法」から「2進法」への変換の方法やな。

これらの計算の方法を覚えておいてね。

忘れたらまたここを見に来るわ。

それでOKよ。
【関連用語】
・ビット/バイト

